NeruIPS 2022년에 나온 논문이다.
source free domain adaptaion의 문제인데 이를 간편하게 Attracting과 dispersing으로 풀었다는데 문제를 한번 보자.
Attracting과 dispersing의 개념은 상반되 개념으로 끌어당김과 분산을 의미하는 바이다.
이 논문에서는 간편한 방법으로 풀었다고 하며 clsutering의 upperbound에 대해서 해결방안을 제시하며 다른 방안으로도 문제를 풀었다.
이 논문의 경우 Srouce free말고도 , domain adaptation, contrastive learning에도 적용할수 있는점이 강점으로 가지고 있는 듯 하다.
Method
우선적으로 사용되어지는 수식은 다음과 같다.
sample dataset $D_t = \{x_i^t\}^{N_t}_{i=1}$
output features : $z_i = f(x) \in \mathbb{R}^C$ , $z_i \in \mathbb{R}^h$
classifier output : $p_i = \delta(g(z_i)) \in \mathbb{R}^C$
softmax : $\delta$
Attracting and Dispersing for Source-free Domain Adaptation
저자는 SFDA의 문제를 attracting와 dispersing으로 풀었으며 이때 $z_i$를 2개의 memory bank를 사용하여 문제를 풀었다. $z_i$에 가까운 set을 KNN으로 $C_i$로 만들고 가깝지 않는 것에 대해서는 $B_i$로 하여 정의를 하였따. 이러한 2개의 memory bank의 경우에서는 계속 하여 update가 되어지며 이러한 $B_i, C_i$에 있는 Prob의 경우에서는 아래의 식과 같이 구성이 되어진다.
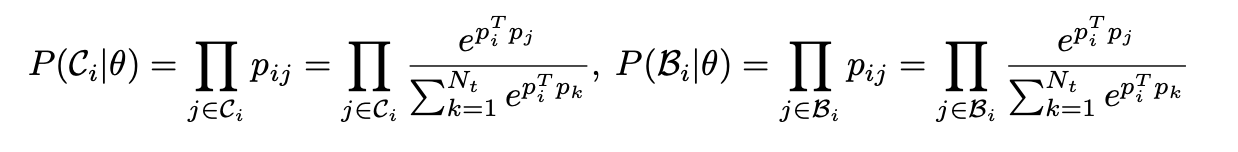
이러한 2개의 prob를 KL loss로 풀게 되었는데 이는 밑의 수식과 같다.

분모의 부분과 분자의 부분은 1로 가까워짐으로 이는 contrastive처럼 동작이 되는데 $P(C_i)$의 경우는 점점 가까워지게 되고 $P(B_i)$의 경우는 $B$와
는 점점 멀어지게 된다.
이러한 수식의 풀이는 밑의와 같이 진행이 되어진다.

이러한 수식은 아주 간편하게 하나의 Loss로 되어진다.

그렇다면 기존의 discriminability (dis) and diversity (div)로 구별이 되어지는 loss는 어떻게 되어지는지 표에서 보자.

Mutual informtaion maximizaing의 경우에서는 다른 논문에서 적용했던 방법론으로 unsupervised clustering에서는 많이 사용이 되어진다. $H(Y|X)$의 unambiguous의 부분은 최소화하고 entropy 부분인 $H(Y)$의 경우는 전체 data에 대한 Entropy를 높여서 ambiguous한 부분을 밀어내는 영향이 있다.
Batch Nuclear-norm Maximization (BNM)의 방법은 Frobenius norm을 사용해서 사용하였으며 second term의 경우에서는 rank로 하여서 구성하였다.
Neighborhood Clustering (NC)의 경우에서는 주변의 KNN의 distance에 대당하는 값의 경우 weight를 주어서 cluster가 되도록 하며 다른 diversity의 부분은 멀게 하는 방법으로 사용이 되어진다.
결과는 아래와 같이 나오게 되어진다.

DA의 방법은 Source data의 접근이 가능해야 MMD같은 방법을 사용할수 있음. 또한 ADDA parameter를 share해서 새로운 adversarial framework를 제시하지만 각 domain마다 다른 mapping을 해서 문제를 풀었음.
특히나 source model에서 나온 Distribution을 전부다 기존의 loss로 shift시킬수 없으니 Information maximization을 시킨다. (신기..)
maximum mean discrepancy (MMD) : source domain 과 target domain간의 discrepancy를 최소화하는것
