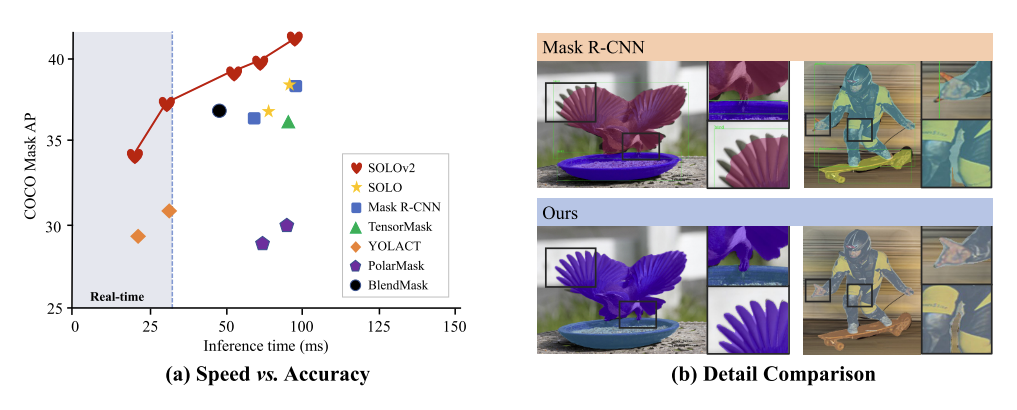
Problem
- Inefficient mask representation and learning
- Not high enough resolution for final mask predictions
- Slow mask NMS
contribution
- First, our new framework is empowered by an efficient and holistic instance mask representation scheme (Head)
- Convolution kernel learning & feature learning
- SOLOv2 significantly reduces inference overhead with our novel matrix non-maximum suppression (NMS) technique.
- NMS with parallel matric operation in one shot.
Method
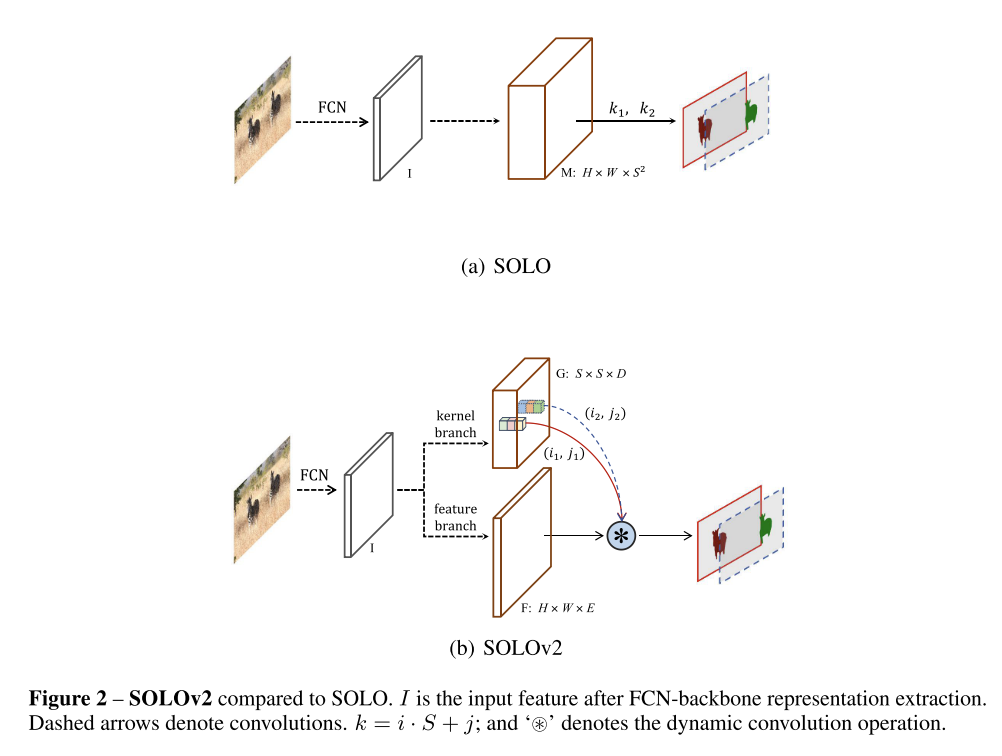
- S^2 때문에 memory가 너무 많이 먹음.
- mask prediction이 정확하지 않음 특히나 큰 resolution에 대해서는 computation cost가 많이 나옴.
- Dynamic Instance segmenation
- 기존의 모델의 경우 FPN(feature pyramid feature)에서 HxWxE만큼의 output이 나옴.
- FCN을 적용하게 되면 S^2의 output으로 나옴. 이 과정을 수식으로 표현하면 M = G * F으로 표현할 수 있음.
- 1x1 convolution을 적용해서 featuere를 줄였을때 전체 M에서 중복되는 부분이 발생함.
- 그렇다면 F & G를 따로 학습을 하게 되면 dynamic하게 사용함으로 segmentation의 location을 효과적으로 찾을 수 있음.
- Mask Kernal Branch (G)
- 각 featuere ouput마다 D-dimentsion마다 아웃풋이 생성이됨
- 이를 해당되는 gride cell (S)로 resize를 시켜준뒤 최종 3x3 convolution을 적용함. 이를 통해 D에 대해서 9E의 feature를 가짐
- 1x1 convolution을 적용하면 D=E는 같아짐.
- Mask feature branch (F)
- 각 feature들은 unified mask를 만듬.
- 1/4 size로 bilinear upsampling를 시켜서 만든 후 sum을 진행함.


- Learning and inference
- Focal loss + Dice loss를 적용
- Matric NMS
- Soft-NMS에서 가져옴
- IOU의 score에 따라서 score를 다르게 주는 방식(IOU 높으면 score를 iou만큼 곱해서 점점 낮게 준다)
- Mask 기준으로 사용하여 decay를 주는 방식
- Soft-NMS에서 가져옴


def matrix_nms(scores, masks, method=’gauss’, sigma=0.5):
# scores: mask scores in descending order (N)
# masks: binary masks (NxHxW)
# method: ’linear’ or ’gauss’
# sigma: std in gaussian method
# reshape for computation: Nx(HW)
masks = masks.reshape(N, HxW)
# pre−compute the IoU matrix: NxN
intersection = mm(masks, masks.T)
areas = masks.sum(dim=1).expand(N, N)
union = areas + areas.T − intersection
ious = (intersection / union).triu(diagonal=1)
# max IoU for each: NxN
ious_cmax = ious.max(0)
ious_cmax = ious_cmax.expand(N, N).T
# Matrix NMS, Eqn.(4): NxN
if method == ’gauss’: # gaussian
decay = exp(−(iousˆ2 − ious_cmaxˆ2) / sigma) else: # linear
decay = (1 − ious) / (1 − ious_cmax)
# decay factor: N
decay = decay.min(dim=0)
return scores ∗ decayEvaluation



반응형
'공부 > paper review' 카테고리의 다른 글
| [Paper review] BOXInst (0) | 2022.12.01 |
|---|---|
| 220622 묵상 (0) | 2022.06.22 |
| [Paper review] SOLO: Segmenting Objects by Locations (0) | 2022.04.07 |
| [논문 리뷰 paper list] (0) | 2022.03.28 |
| [paper review] Multi-class cell detection using Spatial Context Representation (0) | 2021.10.16 |